The order of the reaction = 1/2 + 2
= 2.5
The order of reaction is defined as the sum of the powers of concentrations In the rate law.
The rate of second order reaction can be expressed as rate = k [A]2
The reaction X → Y follows second order kinetics.
Therefore, the rate equation for this reaction will be:
Rate = k [X]2 ________________________ (1)
Let [X] = a mol L-1 , then equation (1) can be written as:
Rate = k [a]2
= ka2
If the concentration of X is increased to three times, then [X] = 3a mol L-1
Now, the rate equation will be:
Rate = k [3a]2
= 9 (ka2)
Hence, the rate of formation will increase by 9 times.
From the question, we can write down the following information:
Initial amount = 5 g
Final concentration = 3 g
Rate constant = 1.15 10 - 3s - 1
We know that for a 1st order reaction,

= 444.38 s
= 444 s (approx)
We know that for a 1st order reaction,
t½ = 0.693 / k
It is given that t1/2= 60 min
k = 0.693 / t½
= 0.693 / 60
= 0.01155 min-1
= 1.155 min-1
Or
k = 1.925 x 10-2 s-1
The rate constant of a reaction is nearly doubled with a 10° rise in temperature. However, the exact dependence of the rate of a chemical reaction on temperature is given by Arrhenius equation,
k = Ae - Ea / RT
Where,
A is the Arrhenius factor or the frequency factor
T is the temperature
R is the gas constant
Ea is the activation energy
It is given that T1 = 298 K
∴T2 = (298 + 10) K
= 308 K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K - 1 mol - 1
Now, substituting these values in the equation:

= 52897.78 J mol - 1
= 52.9 kJ mol - 1
In the given case:
Ea = 209.5 kJ mol - 1 = 209500 J mol - 1
T = 581 K
R = 8.314 JK - 1 mol - 1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as

(i) Given rate = k [NO]2
Therefore, order of the reaction = 2
Dimension of k = Rate / [NO]2
= mol L-1 s-1 / (mol L-1)2
= mol L-1 s-1 / mol2 L-2
= L mol-1 s-1
(ii) Given rate = k [H2O2][I - ]
Therefore, order of the reaction = 2
Dimension of k = Rate / [H2O2][I - ]
= mol L-1 s-1 / (mol L-1) (mol L-1)
= L mol-1 s-1
(iii) Given rate =k [CH3CHO]3/2
Therefore, order of reaction = 3/2
Dimension of k = Rate / [CH3CHO]3/2
= mol L-1 s-1 / (mol L-1)3/2
= mol L-1 s-1 / mol3/2 L-3/2
= L½ mol-½ s-1
(iv) Given rate = k [C2H5Cl]
Therefore,order of the reaction = 1
Dimension of k = Rate / [C2H5Cl]
= mol L-1 s-1 / mol L-1
= s-1
In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:
|
A/ mol L - 1 |
0.20 | 0.20 | 0.40 |
|
B/ mol L - 1 |
0.30 | 0.10 | 0.05 |
|
r0/ mol L - 1 s - 1 |
5.07 × 10 - 5 |
5.07 × 10 - 5 |
1.43 × 10 - 4 |
What is the order of the reaction with respect to A and B?
Let the order of the reaction with respect to A be xand with respect to B be y.
Therefore,

= 1.496
= 1.5 (approximately)
Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.
The following results have been obtained during the kinetic studies of the reaction: 2A + B → C + D
| Experiment |
A/ mol L - 1 |
B/ mol L - 1 |
Initial rate of formation of D/mol L - 1 min - 1 |
| I | 0.1 | 0.1 |
6.0 × 10 - 3 |
| II | 0.3 | 0.2 |
7.2 × 10 - 2 |
| III | 0.3 | 0.4 |
2.88 × 10 - 1 |
| IV | 0.4 | 0.1 |
2.40 × 10 - 2 |
Determine the rate law and the rate constant for the reaction.



The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
| Experiment |
A/ mol L - 1 |
B/ mol L - 1 |
Initial rate/mol L - 1 min - 1 |
| I | 0.1 | 0.1 |
2.0 × 10 - 2 |
| II | -- | 0.2 |
4.0 × 10 - 2 |
| III | 0.4 | 0.4 | -- |
| IV | -- | 0.2 |
2.0 × 10 - 2 |
The given reaction is of the first order with respect to A and of zero order with respect to B.
Therefore, the rate of the reaction is given by,
Rate = k [A]1[B]0
⇒ Rate = k [A]
From experiment I, we obtain
2.0 x 10-2mol L-1min-1= k (0.1 mol L-1)
⇒ k = 0.2 min-1
From experiment II, we obtain
4.0 x 10-2mol L-1min-1= 0.2 min-1[A]
⇒ [A] = 0.2 mol L-1
From experiment III, we obtain
Rate = 0.2 min-1 x 0.4 mol L-1
= 0.08 mol L-1min-1
From experiment IV, we obtain
2.0 x 10-2mol L-1min-1= 0.2 min-1[A]
⇒ [A] = 0.1 mol L-1
(i) Half life, t½ = 0.693 / k
= 0.693 / 200 s-1
= 3.47 ×10 -3 s (approximately)
(ii) Half life, t½ = 0.693 / k
= 0.693 / 2 min-1
= 0.35 min (approximately)
(iii) Half life,t½ = 0.693 / k
= 0.693 / 4 years-1
= 0.173 years (approximately)
Here,
K = 0.693 / t½
= 0.693 / 5730 years-1
It is known that,

= 1845 years (approximately)
Hence, the age of the sample is 1845 years.
The experimental data for decomposition of N2O5
[2N2O5 → 4NO2 + O2]
in gas phase at 318K are given below:
| t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5] mol L-1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log[N2O5] and t.
(iv) What is the rate law ?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
(i)

(ii) Time corresponding to the concentration, 1630x102 / 2 mol L-1 = 81.5 mol L-1 is the half life. From the graph, the half life is obtained as 1450 s.
(iii)
| t/s | 102 × [N2O5] mol L-1 | Log [N2O5] |
| 0 | 1.63 | -1.79 |
| 400 | 1.36 | -1.87 |
| 800 | 1.14 | -1.94 |
| 1200 | 0.93 | -2.03 |
| 1600 | 0.78 | -2.11 |
| 2000 | 0.64 | -2.19 |
| 2400 | 0.53 | -2.28 |
| 2800 | 0.43 | -2.37 |
| 3200 | 0.35 | -2.46 |

(iv) The given reaction is of the first order as the plot, log[N2O5] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N2O5]
(v) From the plot, log[N2O5]
v/s t, we obtain
Slope = -2.46 -(1.79) / 3200-0
= -0.67 / 3200
Again, slope of the line of the plot log[N2O5] v/s t is given by
- k / 2.303
.Therefore, we obtain,
- k / 2.303 = - 0.67 / 3200
⇒ k = 4.82 x 10-4 s-1
(vi) half life is given by,
t½ = 0.693 / k
= 0.639 / 4.82x10-4 s
=1.438 x 103 s
Or we can say
1438 S
Which is very near to what we obtain from graph.

Therefore, 0.7814 μg of 90Sr will remain after 10 years.
Again,

Therefore, 0.2278 μg of 90Sr will remain after 60 Years
For a first order reaction, the time required for 99% completionis
t1 = 2.303/k Log 100/100-99
= 2.303/k Log 100
= 2x 2.303/k
For a first order reaction, the time required for 90% completion is
t2 = 2.303/k Log 100/100-90
= 2.303/k Log 10
= 2.303/k
Therefore, t1 = 2t2
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
For a first order reaction,
t = 2.303/k Log [R] º / [R]
k = 2.303/40min Log 100 / 100-30
= 2.303/40min Log 10 / 7
= 8.918 x 10-3 min-1
Therefore, t1/2 of the decomposition reaction is
t1/2 = 0.693/k
= 0.693 / 8.918 x 10-3 min
= 77.7 min (approximately)
The initial rate of the reaction is
Rate = k [A][B]2
= (2.0 × 10 - 6mol - 2L2s - 1) (0.1 mol L - 1) (0.2 mol L - 1)2
= 8.0 × 10 - 9mol - 2L2s - 1
When [A] is reduced from 0.1 mol L - 1to 0.06 mol - 1, the concentration of A reacted = (0.1 - 0.06) mol L - 1 = 0.04 mol L - 1
Therefore, concentration of B reacted= 1/2 x 0.04 mol L-1 = 0.02 mol L - 1
Then, concentration of B available, [B] = (0.2 - 0.02) mol L - 1
= 0.18 mol L - 1
After [A] is reduced to 0.06 mol L - 1, the rate of the reaction is given by,
Rate = k [A][B]2
= (2.0 × 10 - 6mol - 2L2s - 1) (0.06 mol L - 1) (0.18 mol L - 1)2
= 3.89 mol L - 1s - 1
For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
| t (sec) | P(mm of Hg) |
| 0 | 35.0 |
| 360 | 54.0 |
| 720 | 63.0 |
Calculate the rate constant
The decomposition of azoisopropane to hexane and nitrogen at 543 K is represented by the following equation.
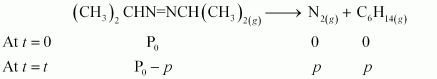
After time, t, total pressure, Pt = (Pº - p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt - Pº
therefore, Pº - p = Pº - Pt - Pº
= 2 Pº - Pt
For a first order reaction,
k = 2.303/t Log Pº / Pº - p
= 2.303/t Log Pº / 2 Pº - Pt
When t = 360 s, k = 2.303 / 360s log 35.0 / 2x35.0 - 54.0
= 2.175 × 10 - 3 s - 1
When t = 720 s, k = 2.303 / 720s log 35.0 / 2x35.0 - 63.0
= 2.235 × 10 - 3 s - 1
Hence, the average value of rate constant is
k = (2.175 × 10 - 3 + 2.235 × 10 - 3 ) / 2 s - 1
= 2.21 × 10 - 3 s - 1
The following data were obtained during the first order thermal decomposition of SO2Cl2at a constant volume.
SO2Cl2(g) → SO2(g) + Cl2(g)
| Experiment |
Time/s - 1 |
Total pressure/atm |
| 1 | 0 | 0.5 |
| 2 | 100 | 0.6 |
Calculate the rate of the reaction when total pressure is 0.65 atm.
The thermal decomposition of SO2Cl2at a constant volume is represented by the following equation.

After time, t, total pressure,Pt = (Pº - p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt - Pº
therefore, Pº - p = Pº - Pt - Pº
= 2 Pº - Pt
For a first order reaction,
k = 2.303/t Log Pº / Pº - p
= 2.303/t Log Pº / 2 Pº - Pt
When t= 100 s,
k = 2.303 / 100s log 0.5 / 2x0.5 - 0.6
= 2.231 × 10 - 3s - 1
When Pt= 0.65 atm,
P0+ p= 0.65
⇒ p= 0.65 - P0
= 0.65 - 0.5
= 0.15 atm
Therefore, when the total pressure is 0.65 atm, pressure of SOCl2 is
pSOCL2 = P0 - p
= 0.5 - 0.15
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k(pSOCL2)
= (2.23 × 10 - 3s - 1) (0.35 atm)
= 7.8 × 10 - 4atm s - 1
The rate constant for the decomposition of N2O5 at various temperatures is given below:
|
T/°C |
0 | 20 | 40 | 60 | 80 |
|
105 X K /S-1 |
0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and 1/T and calculate the values of A and Ea.
Predict the rate constant at 30 º and 50 ºC.
From the given data, we obtain
| T/°C | 0 | 20 | 40 | 60 | 80 |
|
T/K |
273 | 293 | 313 | 333 | 353 |
| 1/T / k-1 |
3.66×10 - 3 |
3.41×10 - 3 |
3.19×10 - 3 |
3.0×10 - 3 |
2.83 ×10 - 3 |
| 105 X K /S-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| In k | -7.147 | -4.075 | -1.359 | -0.577 | 3.063 |
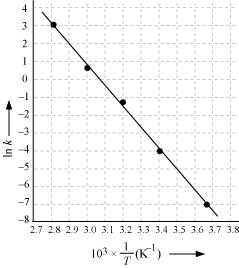
Slope of the line,

In k= - 2.8
Therefore, k = 6.08x10-2s-1
Again when T = 50 + 273K = 323K,
1/T = 3.1 x 10-3 K
In k = - 0.5
Therefore, k = 0.607 s-1
k= 2.418 × 10-5 s-1
T= 546 K
Ea= 179.9 kJ mol - 1 = 179.9 × 103J mol - 1
According to the Arrhenius equation,

= (0.3835 - 5) + 17.2082
= 12.5917
Therefore, A = antilog (12.5917)
= 3.9 × 1012 s - 1(approximately)
k= 2.0 × 110-2 s-1
T= 100 s
[A]o= 1.0 moL - 1
Since the unit of kis s - 1, the given reaction is a first order reaction.
Therefore, k = 2.303/t Log [A]º / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s Log 1.0 / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s ( - Log [A] )
⇒ - Log [A] = - (2.0 x 10-2 x 100) / 2.303
⇒ [A] = antilog [- (2.0 x 10-2 x 100) / 2.303]
= 0.135 mol L - 1 (approximately)
Hence, the remaining concentration of A is 0.135 mol L - 1.
For a first order reaction,
k = 2.303/t Log [R]º / [R]
It is given that, t1/2 = 3.00 hours
Therefore, k = 0.693 / t1/2
= 0.693 / 3 h-1
= 0.231 h - 1
Then, 0.231 h - 1 = 2.303 / 8h Log [R]º / [R]

Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158.
The decomposition of hydrocarbon follows the equation
k = (4.5 x 1011 s-1) e-28000 K/T
Calculate Ea.
The given equation is
k = (4.5 x 1011 s-1) e-28000 K/T (i)
Arrhenius equation is given by,
k= Ae -Ea/RT (ii)
From equation (i) and (ii), we obtain
Ea / RT = 28000K / T
⇒ Ea = R x 28000K
= 8.314 J K - 1mol - 1× 28000 K
= 232792 J mol - 1
= 232.792 kJ mol - 1
Arrhenius equation is given by,
k= Ae -Ea/RT
⇒In k = In A - Ea/RT
⇒In k = Log A - Ea/RT
⇒ Log k = Log A - Ea/2.303RT (i)
The given equation is
Log k = 14.34 - 1.25 104 K/T (ii)
From equation (i) and (ii), we obtain
Ea/2.303RT = 1.25 104 K/T
⇒ Ea =1.25 × 104K × 2.303 × R
= 1.25 × 104K × 2.303 × 8.314 J K - 1mol - 1
= 239339.3 J mol - 1 (approximately)
= 239.34 kJ mol - 1
Also, when t1/2= 256 minutes,
k = 0.693 / t1/2
= 0.693 / 256
= 2.707 × 10 - 3 min - 1
= 4.51 × 10 - 5s - 1
It is also given that, log k= 14.34 - 1.25 × 104K/T

= 668.95 K
= 669 K (approximately)
From Arrhenius equation, we obtain
log k2/k1 = Ea / 2.303 R (T2 - T1) / T1T2
Also, k1 = 4.5 × 103 s - 1
T1 = 273 + 10 = 283 K
k2 = 1.5 × 104 s - 1
Ea = 60 kJ mol - 1 = 6.0 × 104 J mol - 1
Then,

= 297 K = 24°C
Hence, k would be 1.5 × 104 s - 1 at 24°C.
For a first order reaction,
t = 2.303 / k log a / a - x
At 298 K,
t = 2.303 / k log 100 / 90
= 0.1054 / k
At 308 K,
t' = 2.303 / k' log 100 / 75
= 2.2877 / k'
According to the question,
t = t'
⇒ 0.1054 / k = 2.2877 / k'
⇒ k' / k = 2.7296
From Arrhenius equation,we obtain
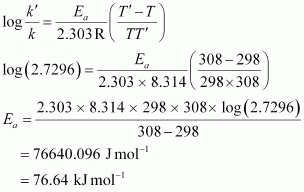
To calculate k at 318 K,
It is given that, A = 4 x 1010 s-1, T = 318K
Again, from Arrhenius equation, we obtain

Therefore, k = Antilog (-1.9855)
= 1.034 x 10-2 s -1
The decomposition of NH3on platinum surface is represented by the following equation.

= 7.5 × 10 - 4mol L - 1s - 1
From Arrhenius equation, we obtain

Hence, the required energy of activation is 52.86 kJ mol - 1.
If pressure is measured in bar and time in minutes, then
Unit of rate = bar min - 1
Rate = k (PCH3OCH3)3/2
⇒ k = Rate / (PCH3OCH3)3/2
Therefore, unit of rate constants (k) = bar min-1 / bar3/2
= bar-½ min - 1
The factors that affect the rate of a reaction areas follows.
(i) Concentration of reactants (pressure in case of gases)
(ii) Temperature
(iii) Presence of a catalyst
Let the concentration of the reactant be [A] = a
Rate of reaction, R = k [A]2 = ka2
(i) If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R = k(2a)2
= 4ka2
= 4 R
Therefore, the rate of the reaction would increase by 4 times.
(ii) If the concentration of the reactant is reduced to half, i.e. [A] = 1/2 a, then the rate of the reaction would be
R = k(1/2a)2
= 1/4 Ka2
= 1/4 R
The rate constant is nearly doubled with a rise in temperature by 10° for a chemical reaction.
The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,
K = Ae -Ea / RT
where, kis the rate constant,
A is the Arrhenius factor or the frequency factor,
R is the gas constant,
T is the temperature, and
Ea is the energy of activation for the reaction
In a pseudo first order hydrolysis of ester in water, the following results were obtained:
| t/s | 0 | 30 | 60 | 90 |
|
[Ester]mol L - 1 |
0.55 | 0.31 | 0.17 | 0.085 |
(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
(i) Average rate of reaction between the time interval, 30 to 60 seconds, = d[ester] / dt
= (0.31-0.17) / (60-30)
= 0.14 / 30
= 4.67 × 10 - 3mol L - 1s - 1
(ii) For a pseudo first order reaction,
k = 2.303/ t log [R]º / [R]
For t= 30 s, k1 = 2.303/ 30 log 0.55 / 0.31
= 1.911 × 10 - 2s - 1
For t = 60 s, k2 = 2.303/ 60 log 0.55 / 0.17
= 1.957 × 10 - 2s - 1
For t= 90 s, k3 = 2.303/ 90 log 0.55 / 0.085
= 2.075 × 10 - 2s - 1
Then, average rate constant, k = k1 + k2+ k3 / 3
= 1.911 × 10 - 2 + 1.957 × 10 - 2 + 2.075 × 10 - 2 / 3
= 1.981 x 10-2 s - 1